\(\triangleright\) Définition de l'énergie mécanique:
\(E_m={{E_p+E_c}}\)
Seules les forces conservatives travaillant sont à prendre en compte
\(\triangleright\) Variation de l'énergie mécanique d'un système
On définit la variation d'énergie mécanique d'un système comme:
$$\Delta E_m={{W^{NC}_{ext}+W^{NC}_{int} }}$$
\(\triangleright\) Définition de l'énergie mécanique d'un système
Un système possède une énergie interne.
$$E_m= {{E_c + E_{p,ext}+ E_{p,int} }}$$
Avec:
- \(E_c\): Energie Cinétique
- \(E_{p,ext}\): energie potentielle extérieur (Forces conservatives et énergie potentielle)
- \(E_{p,int}\): Energie potentielle interne
Théorème de l’énergie mécanique (N corps)
- Pendule simple:
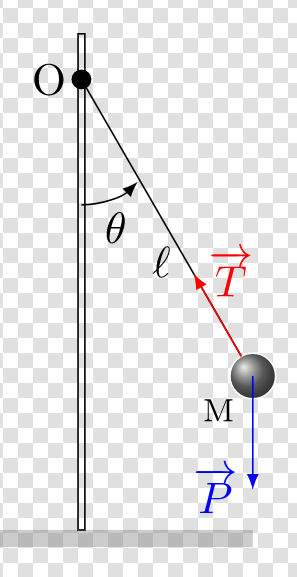
Montrons que l'\(E_m\) du point matériel peut se mettre sous la forme $$E_m=\frac 12 ml^2\theta^2+mgl(1-cos\theta)$$
\(\to\) Resolution:
- Point matériel de masse m
- Réferentiel galiléen
- Base intrinséque \(\{\vec e_n,\vec e_t\}\) ou \(\{\vec i,\vec j,\vec k\}\)
- Frottements négligées
A) Dans la base de Serret-Frenet:
$$\begin{align}&\overrightarrow OM=l(-\vec e_n)=-l\vec e_n
\\ &\vec v=l.\dot\theta.\vec e_t \\ &\textEcrivons le vecteur position dans la base \\ vec i,\vec j, \vec k\:\\ &\overrightarrowOM= l\sin\theta.\vec i-l\cos\theta.\vec k\end{align}$$
B) Energie cinétique:
$$\begin{align}&E_c=\frac 12mv^2=\frac 12m.l^2.\dot\theta^2\\ &\end{align}$$
C) Energie potentielle:
$$\begin{align}&\vec T\perp\vec v\implies\text{ne travail pas pour l'énergie}\\ &\vec P \text{ est une force conservative}\\ &\delta W=\vec F.\vec dl=-dE_p\\ & E_{pp}=\int-\vec F.\vec dl=\int-(-mg)dz=mgz+cst\\ &\text{où }z= -l\cos\theta\\ & E_{pp}=-mgl\cos\theta+cst\\ & \text{On prend le point }O' \text{comme origine de l'}E_{pp}:\\ &E_{pp}=(z=l)=0\implies cst=mgl\\ &\\ &\longrightarrow E_{pp}=mgl(1-\cos\theta)\end{align}$$
- Le ressort:
Montrons que \(E_m=\frac 12 m\dot x^2+\frac 12kx^2\)
\(\longrightarrow\) Resolution:
- Point matériel de masse m
- Referentiel galiléen
- Frottements négligées
- Origine \(O\)
- Repère \(\{\vec i\}\) car mouvement à une dimension
$$\begin{align}&\overrightarrow{OM}=x\vec i\\ &\vec v=\dot x\vec i\\ &\\ &\text{Energie cinétique:}\\ &E_c=\frac 12m\dot x^2\\ &\\ &\text{Energie potentiel:}\\ & \text{R et P ne travaillent pas}\\ & E_p=\int -(-kx)dx=\frac 12kx^2+cst \\ & \text{On choisit comme oigine de l'énergie potentiel le point 0:}\\ &cst=0\end{align}$$
\(\triangleright\) Théroème de l'énergie mécanique:
\(\longrightarrow\) Dans un référentiel galiléen, la variation de l'énergie mécanique est égale au travail des forces non-conservatives.
$$\Delta E_m=W^{NC}$$
- Variation élémentaire:
$$dE_m=\delta W^{NC}$$
\(\longrightarrow\) démonstration:
$$\begin{align}&\text{Notons }F^C, F^{NC}\text{ forces conservative et non conservatives}\\ & \text{TEC entre t et dt:}\\ & dE_c=\delta W=\delta W^c+\delta W^{NC}\\ & \delta W^c=\vec F^c\vec dl=-dE_p\\ & \text {d'où:}\\ &dE_c=\delta W^c+\delta W^{NC}=-dE_p+\delta W^{NC}\\ & dE_c+dEp=\delta W^{NC}\\ & d(E_c+E_p)=\delta W^{NC}\\ & dE_m=\delta W^{NC}\end{align}$$
- Cas de conservation de l'énergie mécanique:
$$E_m=cst\implies dE_m=0\implies\delta W^{NC}=0$$
Il y a conservation de l'énergie mécanique en absence des forces non-conservatives travaillant
\(\triangleright\) Applications:
- Chute libre:
$$\begin{align}& \text{Etat initial:}\\ & E_c=0\\ & E_p=mgh\\ &\\ & \text{Etat final:}\\ &E_c=\frac 12mv_b^2\\ &E_p=0\\ &\lt hline\gt \\ &\Delta E_m=E_m(B)-E_m(A)\\ &=[E_c(B)+E_p(B)]-[E_c(A)+E_p(A)]=0\\ &\frac 12mv_b^2=mgh\\ &v_b=\sqrt{2gh}\end{align}$$
- Ressort:
Determinons l'équation différentielle qui régit le mouvement en utilisant le TEM (pas frottements)
$$\begin{align}&E_m=\frac 12m\dot x^2+\frac 12kx^2=cst\\ &\frac {dE_m}{dx}=0\\ &\frac{dE_m}{dx}=\frac 12 m2\dot x\ddot x+\frac 12k2x\dot x=0\\ &= m\ddot x=-kx\\ &\ddot x=\frac {-k}{m}x\\ & \text{On pose }\omega^2=\frac km\\ & \ddot x=-\omega^2x\end{align}$$
- Toboggan avec frottement solide:
Calculons la vitesse du point matériel sur le tobbogan au point B (final)
$$\begin{align}&\text{Seul le poids est conservatif}\implies E_{pp}=mgz+c\\ & c=0 \text{ en B}\\ &\lt hline\gt \\ &||\vec R_T||=\mu_c||\vec R_N||\\ & R_T=\mu_c.mg\cos\theta=R_N\\ &\\ &\text{TEM entre A et B}\\ &\Delta E_m=W^{NC}\\ &W^{NC}=\int\vec R_T.\vec dl=R_T.AB=\mu_cmg\cos\theta\\ &AB=\frac{h}{\sin\theta}\\ &...\\ & v_b=\sqrt{2gh(1+\frac {\mu_c}{\tan\theta})}\end{align}$$